Saturday morning Sudoku Therapy

It's been a pretty good morning. I've recycled my old magazines and solved a six-star, diabolical Pacific Sudoku (courtesy of the DC Examiner) in under 90 minutes. I didn't think it was going to turn out, because I was using a pen and made the "wrong turn" at the critical guessing point-- but somehow, I was able to "backsolve" from the row with the two conflicting numbers and purge the rest of the puzzle's errors.

The upshot of this is a strangely empowering feeling-- not a "Hey, I'm a genius!" kind of feeling, but more like a "I'm back in the flow/rhythm" sort of feeling. You know, like the sort of day when you can look at something that normally has you flummoxed and suddenly, POW!, it all makes crystal clear sense?

DC Examiner Classic Sudoku

Last weekend, I spent waaaay too much time on the DC Examiner's Classic Sudoku puzzle (6 star difficulty). But that was a week ago, and I've been doing a lot of puzzles. I can't be sure, but I think the programming project might also be causing me to have some improvement as well.

I blew through the 5 star Sudoku Pacific rather easily. Then, I turned my attention to the Sudoku Classic puzzle. At about 30 minutes in, I was pretty sure it was another diabolical puzzle. I inked in the numbers I was certain about, and switched to a pencil. I had to choose between a 6 and an 8 at Row 4, Column 5-- wound up choosing the 6 and discovered about 6 minutes later that path resulted in a conflict. At that point, I had to erase everything from the past six minutes worth of work. That was disheartening. I chose the "8 path" at that point, and was rolling along until an hour and 18 minutes had passed-- and that's when I hit a brick wall.

I've never heard of such a thing as a "double diabolical" puzzle, but I found myself once again in the position of being unable to eliminate any of the remaining possibilities on the grid and having to pick one of two pairs. I suppose it is possible that I overlooked something, but in every row and column the number of empty squares and the number of possible values were equal. At this point, I was so mentally exhausted, I stopped for lunch and took a break to watch an episode of "My Name Is Earl" on the DVR.

Then, I came back and took a new stab at the puzzle. Once again, I couldn't find any way to break the chain of possible values down further-- so I inked in the numbers I'd picked once again (no turning back now, right!?) and choose a path to explore. Fortunately, it turned out to be the correct one. Total time spent on the puzzle: 1 hour and 48 minutes.

Now, I need to get some aspirin and lie down. ;)

Sudoku Dictionary

Since I wasn't making headway on the rest of my "Ultimate Sudoku Solver" program, I decided to pursue the idea of creating a Sudoku dictionary that I had mentioned previously. Solving a Sudoku puzzle can be, in a lot of ways, similar to cracking a password-- so why not create a dictionary of all the possible number combinations that can be in a row or column, and then use something like regular expressions to quickly narrow the range of possibilities a bit.

So, I decided to create my Sudoku dictionary. Manually. It wasn't actually as bad as it sounds. It took about three hours, but there were patterns that developed which allowed me to make good use of Find & Replace and Copy & Paste. [It would have taken even less time if I were actually a TextWrangler power user, instead of a tyro.] With each milestone I reached, the progress jumped dramatically. 24 replacements made . . . 720 replacements made. 350KB became 800 KB. By the time I was done, I had a 3.4 MB plain text file that contains all the possible legal values (note: 362880, to be precise) for one row or column in a Sudoku puzzle.

Now, erm . . . where can I post it? LMAO.

My first thought was Google Docs, but it's a bit too large for that as a text file-- or even as a spreadsheet. I'd like to share it with others, much like I've done with the solution checker, but unless I divide it into segments I don't have anywhere I can post it reliably.

Sudoku Solver Progress, cntd.

My plans for "Black Friday" fell through, so I decided to spend some time optimizing and tweaking my Javascript code for my Sudoku solution testing piece. It's considerably smaller, thanks to a pair of for loops. It's also leaner and uses less processing because it doesn't bother to check the columns if it finds a problem in the rows.

// NAME: sudoku.js
// AUTHOR: Jonah Chanticleer
// VERSION: 2007.11.23
// LICENSE: Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License

function checkRows(S) {

 var sumOfRow = 0;
 var x = 0;

 for (x=0; x<9; x++) {
  sumOfRow = S[x][0] + S[x][1] + S[x][2] + S[x][3]
+ S[x][4] + S[x][5] + S[x][6] + S[x][7] + S[x][8];
  if (sumOfRow != 45) return false;
 }

 return true;
}

function checkCols(S) {

 var sumOfCol = 0;
 var x = 0;

 for (x=0; x<9; x++)
  {
  sumOfCol = S[0][x] + S[1][x] + S[2][x] + S[3][x]
+ S[4][x] + S[5][x] + S[6][x] + S[7][x] + S[8][x];
  if (sumOfCol != 45) return false;
  }

 return true;
}

function testSolution(S) {

 var valid = false;

 valid = checkRows(S);
 if (valid == true) valid = checkCols(S);

 return valid;
}

Sudoku Solution Candidate Testing code

As I mentioned in a previous entry, I've created a prototype in Javascript that tests a solution candidate to see whether it is valid or not. It's just the first piece in my "Ultimate Sudoku Solver" programming project-- more code will be necessary, but this is an important piece.

Usage is pretty straightforward, I think. Add this funtion to your web page, then create a two dimensional array (9x9, of course), populate the cells with valid numbers, and pass the array to my function, like so:

testSolution(puzzle);

The function adds up the sums of the nine columns and nine rows. Each result should equal 45. If so, the function returns true. If not, the function returns false. Yes, there is definitely room for improvement-- e.g. make it faster, or return more info about which row or column is "broken"-- but considering it was a quick coding job, I don't think it's too bad.

Since I've wanted to learn more about Creative Commons Licensing, I decided to release this code (see below) under that licensing paradigm.

<!-- NAME: sudoku.js -->
<!-- AUTHOR: Jonah Chanticleer -->
<-- VERSION: 2007.11.22 -->
<!-- LICENSE: Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License -->



function testSolution(S) {
var row1 = 0;
var row2 = 0;
var row3 = 0;
var row4 = 0;
var row5 = 0;
var row6 = 0;
var row7 = 0;
var row8 = 0;
var row9 = 0;
var col1 = 0;
var col2 = 0;
var col3 = 0;
var col4 = 0;
var col5 = 0;
var col6 = 0;
var col7 = 0;
var col8 = 0;
var col9 = 0;



var row1 = S[0][0] + S[0][1] + S[0][2] + S[0][3] + S[0][4] + S[0][5] + S[0][6] + S[0][7] + S[0][8];

if (row1 == 45) { var row2 = S[1][0] + S[1][1] + S[1][2] + S[1][3] +
S[1][4] + S[1][5] + S[1][6] + S[1][7] + S[1][8];
}

if (row2 == 45) { var row3 = S[2][0] + S[2][1] + S[2][2] + S[2][3] +
S[2][4] + S[2][5] + S[2][6] + S[2][7] + S[2][8];
}

if (row3 == 45) { var row4 = S[3][0] + S[3][1] + S[3][2] + S[3][3] +
S[3][4] + S[3][5] + S[3][6] + S[3][7] + S[3][8];
}

if (row4 == 45) { var row5 = S[4][0] + S[4][1] + S[4][2] + S[4][3] +
S[4][4] + S[4][5] + S[4][6] + S[4][7] + S[4][8];
}

if (row5 == 45) { var row6 = S[5][0] + S[5][1] + S[5][2] + S[5][3] +
S[5][4] + S[5][5] + S[5][6] + S[5][7] + S[5][8];
}

if (row6 == 45) { var row7 = S[6][0] + S[6][1] + S[6][2] + S[6][3] +
S[6][4] + S[6][5] + S[6][6] + S[6][7] + S[6][8];
}

if (row7 == 45) { var row8 = S[7][0] + S[7][1] + S[7][2] + S[7][3] +
S[7][4] + S[7][5] + S[7][6] + S[7][7] + S[7][8];
}

if (row8 == 45) { var row9 = S[8][0] + S[8][1] + S[8][2] + S[8][3] +
S[8][4] + S[8][5] + S[8][6] + S[8][7] + S[8][8];
}


if (row9 == 45) { var col1 = S[0][0] + S[1][0] + S[2][0] + S[3][0] + S[4][0] + S[5][0] + S[6][0] + S[7][0] + S[8][0];
}

if (col1 == 45) { var col2 = S[0][1] + S[1][1] + S[2][1] + S[3][1] +
S[4][1] + S[5][1] + S[6][1] + S[7][1] + S[8][1];
}

if (col2 ==45) { var col3 = S[0][2] + S[1][2] + S[2][2] + S[3][2] +
S[4][2] + S[5][2] + S[6][2] + S[7][2] + S[8][2];
}

if (col3==45) { var col4 = S[0][3] + S[1][3] + S[2][3] + S[3][3] +
S[4][3] + S[5][3] + S[6][3] + S[7][3] + S[8][3];
}

if (col4==45) { var col5 = S[0][4] + S[1][4] + S[2][4] + S[3][4] +
S[4][4] + S[5][4] + S[6][4] + S[7][4] + S[8][4];
}

if (col5==45) { var col6 = S[0][5] + S[1][5] + S[2][5] + S[3][5] +
S[4][5] + S[5][5] + S[6][5] + S[7][5] + S[8][5];
}

if (col6==45) { var col7 = S[0][6] + S[1][6] + S[2][6] + S[3][6] +
S[4][6] + S[5][6] + S[6][6] + S[7][6] + S[8][6];
}

if (col7==45) { var col8 = S[0][7] + S[1][7] + S[2][7] + S[3][7] +
S[4][7] + S[5][7] + S[6][7] + S[7][7] + S[8][7];
}

if (col8 == 45) { var col9 = S[0][8] + S[1][8] + S[2][8] + S[3][8] +
S[4][8] + S[5][8] + S[6][8] + S[7][8] + S[8][8];
}

if (col9 ==45) { return true; }
else { return false; }
}

Sudoku Solver Progress

Decided to take a tentative stab at creating "the ultimate Sudoku Solving Program" (snort!) tonight. Wound up prototyping a function in Javascript that checks a solution candidate and returns true if it is valid or false if it is not valid. I know, using Javascript for the whole program would be lame, but for quick prototyping one function it wasn't too bad.

I'm actually pleasantly surprised how well it turned out. I pass the function an array, and voila!

It's funny, but the more I think about this, the more I realize I was wrong in my initial assumptions. This happens for me a lot-- I think I understand something, learn more about it and think about what I've learned, only to realize I was wrong and have to revise my understanding. Problem is, I was wrong in that means the program should be even easier/faster because there are fewer possibilities to sort through than I thought.

I originally stated that there were 81 cells with 9 possible variables, and then revised it downwards based on the average number of givens provided in a puzzle to something like 9 to the 53rd power. It's actually less than that.

Each row has to have the numbers 1 through 9, with no repeats. It's not 81 cells with 9 possible variables- it's a subset of that because each row and column must be a combination of the digits 1 through 9*. I have no idea how to represent that mathematically, but I'm pretty sure that brings the number of total possibilities down considerably.

* for example: 123456789, 234567891, 345678912, etc. but never 111111111, 111111112, etc.

Sudoku Solver Program Idea

If I keep writing about Sudoku all the time, people will think I'm obsessed. Or boring. I'm not sure which is worse. Obsessed people have some possibility of being freakishly intriguing to a small audience that shares the same interest/hobby. Boring is just . . . well, boring.

I digress.

Tonight, I find myself preoccupied with the idea of creating a computer program that solves Sudoku puzzles-- including diabolicals. I haven't tested every single solver program in existence, obviously, but the ones I have seen don't appear to solve diabolical Sudoku puzzles. At first, this made sense-- the program is applying the various solving techniques (lone number, hidden pairs, etc.) and takes the puzzle as far as it can go with those techniques. Once the techniques stop producing results, the process has no choice but to stop.

But computers aren't humans, and vice versa.

Instead of trying to make the computer mimic human solving techniques and processes, it makes sense to capitalize on the unique strength of the computer's raw computational power. There are 81 cells in a typical Sudoku puzzle, with 9 possible variables in each cell-- that's 9 to the 81st power (or, um . . . 1.96627050476e+77 for those playing along at home). I know that seems like a lot, but with advances in processor speeds, distributed clients, and a smart approach, it isn't completely impossible. Right? Also, don't forget that the values of some of the squares are given at the start (28 given clues in yesterday's diabolical puzzle), so it's more like 9 to the 53 power (aka 3.75710212614e+50).

It's basically a multi-dimensional array, 9 by 9. It helps to think of a series of car tripometers when trying to visualize this-- except each tripometer has nine places, and they are stacked one right above the other. You increment the value of the last cell, and then you perform a series of 18 checksums-- one for each row, and one for each column. If the checksums each add up to 45, then you have a valid sudoku solution. If not, then you know there's at least one number that is wrong, you increment the number again and start over. Humans don't have the speed or patience to pull off such maneuvers-- but computers are fantastic at this sort of thing.

You could do it as a series of 81 nested for loops as well, I suppose, but that'd be crass and ugly. This reminds me of a program I wrote years ago that generated letter combinations for telephone numbers to help people find "vanity" numbers for their phones. Same concept, except you'd be running the process on nine digit numbers instead of seven.

If you really wanted to make it fast, I think you could create a "dictionary" of valid Sudoku puzzles-- in other words, run the program and let it generate all the possible valid combinations of numbers for all possible complete Sudoku puzzles (much like password cracking programs use dictionaries to assist their attacks). Then, all you'd need to do is run a match against the given clues and filter out all the solutions that don't match the values and positions of those clues, and-- voila! -- you have your solution. Of course, storing an array of that size (in RAM or hard drive space) might be problematic.

There must be something wrong in one of my assumptions. It can't possibly be *that* easy, or someone else would have already done it. The total number of possibilities (with 28 provided clues) multiplied by 18 checksum operations is 6.76278382705e+51. Of course, you wouldn't carry out all 18 checksums for every possible combination-- you'd stop running checksums as soon as the first one didn't total 45.

What language would you choose to write something like this in? Jeez, almost every programming language I know is web-oriented these days. That's certainly not too practical for this sort of operation. Maybe it's time I dusted off those old C programming skills and see if I can pull this off.

If anyone's interested in taking a shot at this with me, drop me a line.

DC Examiner's Diabolical Sudoku Classic Puzzle

Our local newspaper, the DC Examiner, recently began running two Sudoku puzzles each day-- Sudoku Classic and Sudoku Pacific. Generally speaking, the Monday puzzles are easy and the difficulty level progresses through the week. By the time you get to the weekend edition, you are looking at maximum skill level puzzles. I know my Sudoku solving techniques are incomplete, so I've been drilling myself with these puzzles to try to force myself to improve.

I could be mistaken, but I think the folks in charge of the Examiner's "Games!" page decided to throw us a curve ball this weekend by featuring a "diabolical" puzzle for the Sudoku Classic (shown below). It's marked with 6 out of 6 stars, and about two-thirds of the way through working the puzzle, you reach a point where it becomes impossible to eliminate any more possibilities.



You don't see many diabolical Sudoku puzzles in mainstream newspapers these days. (It tends to upset the so-called Sudoku purists who insist that all puzzles must be solved by logic alone and should never involve any guesswork.) There is a technique called "Ariadne's thread", which I have not mastered, that might address such situations-- but let's be honest here, it amounts to picking a cell with only two possible values, choosing one of those values and solving forwards from there until you either encounter a conflict or solve the puzzle. If you do find a conflict, you erase your way "backwards" to the point before you picked that value, and then you select the other option and progress forwards. Using a photo copier or different colored pencils makes this process much easier.

Easy is relative in Sudoku

The DC Examiner now appears to carry two Sudoku puzzles a day, instead of just one. What's interesting to me, is that even though both puzzles are labeled as one out of five stars in their difficult rating, I found one of the puzzles far more diffficult and time consuming to solve than the other.

The "Pacific Sudoku" was truly easy and I was able to solve it in less than ten minutes, while the "Sudoku classic" was much more difficult for me to crack and took the better part of an hour.

You would think that an easy puzzle is an easy puzzle, wouldn't you?

Except, the more I think about it, the more I think this is a fallacy.

Let's say there are (just for the sake of argument) ten methods a person can use to solve a sudoku puzzle. There isn't one single method that can solve an entire puzzle all by itself; you have to combine at least two methods in order completely solve a puzzle. If all methods worked equally well on all puzzles, then it would be possible to come up with an "objective" difficulty rating.

The problem is that different techniques work on different puzzles with varying degrees of effectiveness. In other words, methods 1 and 3 might work fantastic on one puzzle, but leave significant gaps on a second puzzle.

If you happen to know the two (or three, or however many) techniques that are particularly effective on that specific puzzle, then the puzzle might be easy in the truest sense of the word. But, if you are missing one of the techniques that is particularly effective on that puzzle, and have to "fall back" and rely upon a lesser technique, then you must expend more effort to crack the puzzle's structure.

So, unless you know ALL of the sudoku puzzle cracking techniques, the ratings will appear uneven. (This begs the question, can Sudoku puzzles be crafted in such a way to favor certain solving techniques? I don't know, nor can I think of a way to test that hypothesis at this time.)

The only thing I've managed to learn today is that, from a subjective standpoint, the difficulty ratings on a Sudoku puzzle appear relative to the number of techniques that a person knows. Until you know all the solving techniques, the ratings will seem radically uneven.

Naturally, this begs the question-- how can you learn all of the Sudoku solving techniques?

Sunday Sudoku

When I first started solving Sudoku puzzles, I used a "brute force" approach. I wrote tiny numbers in every square for every possible value that square could have. Invariably, I would find one or two squares that could only have a single value (e.g. last row, fourth cell from the left can only be a 2).

This discovery would cause me to go back and eliminate all the 2's from that same column and row, which would usually give me another cell that could only be a single value. The process tends to sustain itself, as you can see. It's actually a successful strategy, but it's labor intensive, tedious and takes up a lot of time. Who wants to spend an hour a day or more working sudoku puzzles?

So, you begin to find other tricks (from trial and error, or talking with other people who do sudoku puzzles, or reading books on the subject) that cut down on the time and effort. For example, I can see that the value of the fourth column, fourth row has to be a 1 because the 1's in the fifth and sixth rows make it impossible for any other cell in the middle square to have a value of 1. Since each square has to contain one cell with the value of 1, the process of elimination makes it necessary for the fourth column, fourth row cell to be 1.

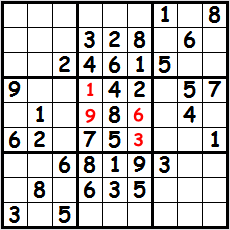Likewise, the 9 in the sixth column makes it impossible for the two cells above it to have a value of 9. The only cell left is the fourth column, fifth row. The only two numbers remaining for the center square are 3 and 6, and the 6 in the sixth row makes that pretty obvious. See, we've solved the entire center square and I didn't have to write down each possible value for the four empty cells in order to do it. There's something to be said for techniques that save time and effort.

I must admit I do still revert back to the "brute force" approach when faced with puzzles of great difficulty. I suspect there are probably other tricks and techniques out there that I am not yet aware of. If I could add a few more of those to my proverbial toolkit, I'd probably be faster/more proficient at solving these harder puzzles.

Sudoku Sunday

Last week, I posted a 5-star difficulty Sudoku puzzle, so I figured I'd better post a simple one this time around.

Enjoy!

Sudoku Sunday

This puzzle appeared in the 4/21 DC Examiner; it has a difficulty rating of five stars. I'm including it here because I found some interesting stuff going on in the bottom left corner.

Basically, I'd gone through the "brute force" method (i.e. figuring out the possible values for each square and annotating them) and found the same three numbers (e.g. 1,2 and 6) repeated in three cells in a row. Although I couldn't tell which number appeared in which cell, I knew that no other cells in that row could use those same numbers. I'd seen that same approach/technique with pairs of number in adjacent cells before, but never triples.

The solution is here for those of you who don't have the time or patience to work through it.